
| 闺蜜小说网 历史小说 武侠小说 网游小说 乡村小说 仙侠小说 竞技小说 耽美小说 重生小说 官场小说 穿越小说 科幻小说 灵异小说 |
| 小说排行榜 玄幻小说 都市小说 军事小说 推理小说 校园小说 短篇文学 言情小说 同人小说 架空小说 经典名著 综合其它 总裁小说 |
| 好看的小说 双向暗恋 滛糜之局 曾照云归 宠媳无边 深闺滛情 宫门滛后 滟妇怀舂 精养父女 爱卻之牢 衣我以夜 热门小说 全本小说 |
|
明史是张廷玉等创作的完结历史小说作品 |

|
|
| 闺蜜小说网 > 历史小说 > 明史 作者:张廷玉等 | 书号:10209 时间:2017/3/26 字数:10591 |
| 上一章 章十二 下一章 ( → ) | |
| 历六 大统历法三下(推步) ▲步  食 食 周⽇二十七⽇二十一刻二二二四。半之为 周⽇二十七⽇二十一刻二二二四。半之为 中⽇。 中⽇。 终度三百六十三度七九三四一九六。半之为 终度三百六十三度七九三四一九六。半之为 中⽇度。 中⽇度。正  度三百五十七度四六。 度三百五十七度四六。中  度一百八十八度零五。 度一百八十八度零五。前准一百六十六度三九六八。 后准一十五度五。  差二⽇三一八三六九。 差二⽇三一八三六九。 望一十四⽇七六五二九六五。 望一十四⽇七六五二九六五。⽇食 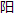 历限六度。定法六十。 历限六度。定法六十。⽇食 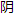 历限八度。定法八十。 历限八度。定法八十。月食十三度五分。定法八十七。 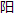 食限(视定朔⼊ 食限(视定朔⼊ 。) 。)零⽇六零已下 一十三⽇一零已上 在一十四⽇,不问小余,皆⼊食限。 一十五⽇二零已下 二十五⽇六零已上 在二十六⽇、二十七⽇,不问小余,皆⼊食限。 ▲ 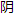 食限(视定望⼊ 食限(视定望⼊ 。) 。)一⽇二零已下 一十二⽇四零已上 在零⽇一十三⽇,不问小余,皆⼊食限。又视定朔小余在⽇出前、⽇⼊后二十分已上者,⽇食在夜。定望小余在⽇⼊前、⽇出后八刻二十分已上者,月食在昼。皆不必布算。 推⽇食用数 经朔 盈缩历 盈缩差 迟疾历 迟疾差 加减差 定朔 ⼊  凡分(以上皆全录之。)定⼊迟疾历(以加减差,加减迟疾即是。)迟疾定限(置定⼊迟疾历,以⽇转限一十二限二十分乘之,小余不用。)定限行度(以定限,取立成內行度,迟用迟,疾用疾,內减⽇行分八分二十秒,得之。)⽇出分(以盈缩历,从立成內取之,下同。)⽇⼊分半昼分(取立成內昏分,减去五千二百五十分,得之。)岁前冬至时⻩道宿次 凡分(以上皆全录之。)定⼊迟疾历(以加减差,加减迟疾即是。)迟疾定限(置定⼊迟疾历,以⽇转限一十二限二十分乘之,小余不用。)定限行度(以定限,取立成內行度,迟用迟,疾用疾,內减⽇行分八分二十秒,得之。)⽇出分(以盈缩历,从立成內取之,下同。)⽇⼊分半昼分(取立成內昏分,减去五千二百五十分,得之。)岁前冬至时⻩道宿次推  常度 置有食之朔⼊ 常度 置有食之朔⼊ 凡分,以月平行度乘之,即得。 凡分,以月平行度乘之,即得。推  定度 置 定度 置 常度,以朔下盈缩差盈加缩减之,即得。 常度,以朔下盈缩差盈加缩减之,即得。推⽇食正  限度 视 限度 视 定度在七度已下,三百四十一度已上者,食在正 定度在七度已下,三百四十一度已上者,食在正 。在一百七十五度已上,二百零二度已下者,食在中 。在一百七十五度已上,二百零二度已下者,食在中 。不在限內不食。 。不在限內不食。推中前中后分 视定朔小余,在半⽇周已下,用减半⽇周,余为中前分。在半⽇周已上,减去半⽇周,余为中后分。 推时差 置半⽇击,以中前、中后分减之,余以中后分乘之,所得以九千六百而一为时差。在中前为减,中后为加。 推食甚定分 置定朔小余,以时差加减之,即得。 推距午定分 置中前、中后分,加时差即得。但加不减。 推食甚⼊盈缩历 置原得盈缩历,加⼊定朔大余及食甚定分,即得。 推食甚盈缩差 依步气朔求之。 推食甚⼊盈缩历行定度 置食甚⼊盈缩历,盈缩差,盈加缩减之,即得。 推南北凡差 视食甚人盈缩历行定度,在周天象限已下为初限,已上与半岁周相减为末限。以初末限自之,如一千八百七十度而一,得数,置四度四十六分减之,余为南北凡差。 推南北定差 置南北凡差,以距午定分乘之,如半昼分而一,以减凡差,余为南北定差。若凡差数少,即反减之。盈初缩末食在正  为减,中 为减,中 为加。缩初盈末,食在正 为加。缩初盈末,食在正 为加,中 为加,中 为减。如系凡差反减而得者,则其加减反是。 为减。如系凡差反减而得者,则其加减反是。推东西凡差 置半岁周,减去食甚⼊盈缩历行定度,余食甚⼊盈缩历行定度乘之,以一千八百七十除之为度,即东西凡差。 推东西定差 置东西凡差,以距午定分乘之,如二千五百度而一,视得数在东西凡差以下,即为东西定差。若在凡差已上,倍凡差减之,余为定差。盈历中前,缩历 后者,正  减,中 减,中 加。盈历中后,缩中前者,正 加。盈历中后,缩中前者,正 加,中 加,中 减。 减。推正  中定限度 视⽇食在正 中定限度 视⽇食在正 者置正 者置正 度,在中 度,在中 者置中 者置中 度,以南北东西二定差加减之,即得。 度,以南北东西二定差加减之,即得。推⽇食⼊ 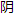 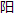 历去闪前后度 视 历去闪前后度 视 定在正 定在正 定限度已下,减去 定限度已下,减去 定度,余为 定度,余为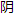 历 历 前度。已上,减去正 前度。已上,减去正 定限度,余为 定限度,余为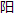 历 历 后度。在中 后度。在中 定限度已下,减去 定限度已下,减去 定度,余为 定度,余为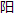 历闪前度。已上,减去中 历闪前度。已上,减去中 定限度,余为 定限度,余为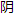 历后度。若 历后度。若 定在七度已下者加 定在七度已下者加 终度,减去正 终度,减去正 定限度,余为 定限度,余为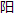 历 历 后度。 后度。推⽇食分秒 在 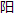 历者,置 历者,置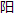 食限六度,减去 食限六度,减去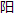 历 历 前、 前、 后度,(不及减者,不食。) 后度,(不及减者,不食。)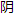 历同。余以定法六十而一。在 历同。余以定法六十而一。在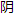 历者,置 历者,置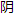 食限八度,减去 食限八度,减去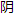 历 历 前、 前、 后度,余以定法八十而一,即得。 后度,余以定法八十而一,即得。推定用分 置⽇食分秒与二十分相减相乘,为开方积。以平方法开之,为开方数。用五千七百四十分(七因八百二十分也。)乘之,如定限行度而一,即得。 推初亏复圆时刻 置食甚定分,以定用分减为初亏,加为复圆。各依发敛加时,即时刻。 推⽇食起复方位 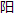 历初亏西南,甚于正南,复于东南。 历初亏西南,甚于正南,复于东南。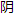 历初亏西北,甚于正北,复于东北。若在八分以上,不分 历初亏西北,甚于正北,复于东北。若在八分以上,不分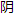 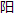 历皆亏正西,复东位。(据午地而论) 历皆亏正西,复东位。(据午地而论)推食甚⽇躔⻩道宿次 置食甚⼊盈缩历行定度,在盈就为定积度,在缩加半岁周为定积度。置定积度,以岁前冬至加时⻩道⽇度加之,満⻩道积度钤去之,至不満宿次即食甚⽇躔。 推⽇带食 视初亏食甚分,有在⽇出分已下,为晨刻带食。食甚复圆分,有在⽇⼊分已上,为昏刻带食。在晨置⽇出分,在昏昏置⽇⼊分,皆以食甚分与之相减,余为带食差。置带带差,以⽇食分秒乘之,以定用分而一,所得减⽇食分秒,余为所见带食分秒。 ▲推月食用数 经望 盈缩历 盈缩差 迟疾历 迟疾差 加减差 定望 ⼊  凡分 凡分定⼊迟疾历 定限 定限行度 晨分 ⽇出分 昏分 ⽇⼊分 限数 ▲岁前冬至加时⻩道宿次 推  常度 置望下⼊ 常度 置望下⼊ 凡分,乘月平行,如⽇食法。 凡分,乘月平行,如⽇食法。推  定度 置 定度 置 常度,以望下盈缩差盈加缩减之即得。不及减者,加 常度,以望下盈缩差盈加缩减之即得。不及减者,加 终度减之。 终度减之。推食甚定分 不用时差,即以定望分为食甚分。 推食甚⼊盈缩历行定度 法同推⽇食。 推月食⼊ 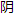 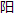 历 视 历 视 定度在 定度在 中度已下为 中度已下为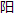 历,已上减去 历,已上减去 中度,余为队历。 中度,余为队历。推  前 前 后度 视所得⼊ 后度 视所得⼊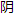 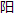 历,在后准已下为 历,在后准已下为 后,在前准已上置 后,在前准已上置 中度减之,余为 中度减之,余为 前。 前。推月食分秒 置月食限一十三度零五,减去前  后度,(不及减者不食。)馀以定法八十七分而一,即得。 后度,(不及减者不食。)馀以定法八十七分而一,即得。推月食用分 置三十分,与月食分秒相减相乘,为开方积。依平方法开之,为开方数。又以四千九百二十(乃六因八百二十分数。)分乘之,如定限行度而一,即得。 推月食三限(初亏、食甚、复圆。)时刻 置食甚分定分,以用分减为初亏,加为复圆。依发敛得时刻如⽇食。 推月食五限时刻 月食十分已上者,用五限推之,初亏、食既、食甚、生光、复圆也。置月食分秒,减去十分,余与十分相减相乘,为开方积。平方开之,为开方数。又以四千九百二十分乘之,如定限行度而一为既內分。与定用分相减,余为既外分。置食甚定分,减既內分为既分,又减既外分为初亏分。再置食甚定分,加既內分为生光分,又加既外分为复圆分。各依以敛得时刻。 推更点 置晨分们之,五分之为更法,又五分之为点法。 推月食⼊更点 各置三限或五限,在昏分已上减去昏分,在晨分已下加⼊晨分,不満更法为初更,不満点法为一点,以次求之,各得更点之数。 推月食起复方位 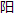 历初亏东北,甚于正北,复于西北。 历初亏东北,甚于正北,复于西北。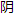 历初亏东南,甚于正南,复于西南。若食在八分已上者,皆初亏正东,复于正西。 历初亏东南,甚于正南,复于西南。若食在八分已上者,皆初亏正东,复于正西。推食甚月离⻩道宿次 置食甚⼊盈缩历定度,在盈加半周天,在缩减去七十五秒为定积度。置定积度,加岁前冬至加时⻩道⽇度,以⻩道积度钤去之,即得。 推月带食 视初亏、食甚、复圆等分,在⽇⼊分以下,为昏刻带食。在⽇出分已上,为晨刻带食。(推法同⽇食。) ▲步五星 历度三百六十五度二五七五,半之为历中,又半之为历策。 木星 合应二百四十三万二三零一。(置中积三亿七千六百一十九万七七五,加辛巳合应一百一十九七二六,得三亿七行七百三十七万九五零一,満木星周率去之,余为《大统》合应。) 历应五百三十八万二五七七二二一五。(置中积,加辛巳历应一千八百九十九万九四八一,得三亿九千五百一十九万娥二五六,満木星历率去之,余为《大统》历应。) 周率三百九十八万八八。 历率四千三百三十一万二九四六八六五。 度率一十一万八五八二。 伏见一十三度。 段目 段⽇ 平度 限度 初行率 合伏 一十六⽇八六 三度八六 二度九三 二十三分 晨疾初 二十八⽇ 六度二一 四度四六 二十二分 晨疾末 二十八⽇ 五度五一 四度四六 二十二分 晨迟初 二十八⽇ 四度三一 三度二八 一十八分 晨迟末 二十八⽇ 一度九一 一度四五 一十二分 晨留 二十四⽇ 晨退 四十六⽇五八 四度八八一二五 零度三二八七五 夕退 四十六⽇五八 四度八八一二五 零度三二八七五 一十六分 夕留 二十四⽇ 夕迟初 二十八⽇ 一度九一 一度四五 夕迟末 二十八⽇ 四度三一 三度二八 一十二分 夕疾初 二十八⽇ 五度五一 四度一九 一十八分 夕疾末 二十八⽇ 六度一一 四度四六 二十一分 夕伏 一十六⽇八六 三度八六 二度九三 二十二分 火星 合应二百四十零万一四。(置中积,加辛巳合应五十六万七五四五,得三亿七千六百七十六万七三二,満火星周率去之,为《大统》合应。中积见木星,五星并同。) 历应三百八十四万五七八九三五。(置中积,加辛巳历应五百四十七万二九三八,得三亿八千一百六十七万二七一三,満火星历率去之。) 周率七百七十九万九二九。 历率六百八十六万九五八零四三。 度率一万八八零七五。 伏见一十九度。 段目 段⽇ 平度 限度 初行率 合伏 六十九⽇ 五十度 四十六度五零 七十三分 晨疾初 五十九⽇ 四十一度八零 三十八度八七 七十二分 晨疾末 五十七⽇ 三十九度零八 三十六度三四 七十分 晨次疾初 五十三⽇ 三十四度一六 三十一度七七 六十七分 晨次疾末 四十七⽇ 二十七度零四 二十五度一五 六十二分 晨迟初 三十九⽇ 一十七度七二 一十六度四八 五十三分 晨初末 二十九⽇ 六度二零 五度七七 三十八分 晨留 八⽇ 晨退 二十八⽇六九四五 八度六五六七五 六度四六三二五 夕退 二十八⽇九四六五 八度六五六七五 六度四六三二五四十四分 夕留 八⽇ 夕迟初 二十九⽇ 六度二零 五度七七 夕迟末 三十九⽇ 一十七度七二 一十六度四八 三十八分 夕次疾初 四十七⽇ 二十七度零四 二十五度一五 五十三分 夕迟疾末 五十三⽇ 三十四度一六 三十一度七七 六十二分 夕疾初 五十七⽇ 三十九度零八 三十六度三四 六十七分 夕疾末 五十九⽇ 四十一度八零 三十八度八七 七十分 夕伏 六十九⽇ 五十度 四十六度五零 七十二分 土星 合应二百零六万四七三四。(置中积,加辛巳合应一十七万五四六三,得三亿七千六百三十七万五四一八,満土星周率去之。) 历应一亿零六百零零万三七九九零二。(置中积,加辛巳历应五千二百二十四万零五六一,得四亿二千八百四十四万零三三六,満土星历率去之。) 周率三百七十八万零九一六。 历率一亿零七百四十七万八八四五六六。 度率二十九万四二五五。 伏见一十八度。 段目 段⽇ 平度 限度 初行率 合伏 二十⽇四零 二度四零 一度四九 一十二分 晨疾 三十一⽇ 三度四零 二度一一 一十一分 晨次疾 二十九⽇ 二度七五 一度七一 一十分 晨迟 二十六⽇ 一度五零 零度八三 八分 晨留 三十⽇ 晨退 五十二⽇四六五八 三度六二五四五 零度二八四五五 夕退 五十二⽇四六五八 三度六二五四五 零度二八四五五 一十分 夕留 三十⽇ 夕迟 二十六⽇ 一度五零 零度八三 夕次疾 二十九⽇ 二度七五 一度七一 八分 夕疾 三十一⽇ 三度四零 二度一一 一十分 夕伏 二十⽇四零 二度四零 一度四九 一十一分 金星 合应二百三十七万九四一五。(置中积,加辛巳合应五百七十一万六三三零,得三亿八千一百九十一万六一零五,満金星周率去之。) 历应一十零万四一八九。(置中积,加辛巳历应一十一万九六三九,得三亿七千六百三十一万九四一四,満金星历率去之。) 周率五百八十三万九零二六。 历率三百六十五万二五七五。 度率一万。 伏见一十度半 段目 段⽇ 平度 限度 初行率 合伏 三十九⽇ 四十九度五零 四十七度四六 一度二七五 夕疾初 五十二⽇ 六十五度五零 六十三度零四 一度二七五 夕疾末 四十九⽇ 六十一度 五十八度七一 一度二五五 夕次疾初 四十二⽇ 五十度二五 四十八度三六 一度二三五 夕次疾末 三十九⽇ 四十二度五零 四十度九零 一度一六 夕迟初 三十三⽇ 二十七度 二十五度九九 一度零二 夕初末 一十六⽇ 四度二五 四度零九 六十二分 夕留 五⽇ 夕退 一十⽇九五三一 三度六九八七 一度五九一三 夕退伏 六⽇ 四度三五 一度六三 六十一分 合退伏 六⽇ 四度三五 一度六三 八十二分 晨退 一十⽇九五三一 三度六九八七 一度五九一三 六十一分 晨留 五⽇ 晨迟初 一十六⽇ 四度二五 四度零九 晨迟末 三十三⽇ 二十七度 二十五度九九 六十二分 晨次疾初 三十九⽇ 四十二度五零 四十度九零 一度零二 晨次疾末 四十二⽇ 五十度二五 四十八度三六 一度一六 晨疾初 四十九⽇ 六十一度 五十八度七一 一度二三五 晨疾末 五十二⽇ 六十五度五零 六十三度零四 一度二五五 晨伏 三十九⽇ 四十九度五零 四十七度四六 一度二六五 ⽔星 合应三十零万三二一二。(置中积,加辛巳合应七十零万零四三七,得三亿七千六百九十零万零二一二,満⽔星周率去之。) 历应二百零三万九七一一。(置中积,加辛巳历应二百零五万五一六一,得三亿七千八百二十五万四九三六,満⽔星历率去之。) 周率一百一十五万八七六。 历率三百六十五万二五七五。 度率一万。 晨伏夕见一十六度半。 夕伏晨见一十九度。 段目 段⽇ 平度 限度 初行率 合伏 一十七⽇七五 三十四度二五 二十九度零八 二度一五五八 夕疾 一十五⽇ 二十一度三八 一十八度一六 一度七零三四 夕迟 一十二⽇ 一十度一二 八度五九 一度一四七二 夕留 二⽇ 夕退伏 一十一⽇一八八 七度八一二 二度一零八 合退伏 一十一⽇一八八 七度八一二 二度一零八 一度零三四六 晨留 二⽇ 晨迟 一十二⽇ 一十度一二 八度五九 晨疾 一十五⽇ 二十一度三八 一十八度一六 一度一四七二 晨伏 一十七⽇七五 三十四度二五 二十九度零八 一度七零三四 推五星前后合 置中积,加合应,満周率去之,余为前合。再置周率,以前合减之,于为后合。如満岁周去之,即其年无后合分。 推五星中积⽇中星度 置各星后合,既为合伏下中积中星。(命为⽇,曰中积。命为度,曰中星。)累加段⽇,为各段中积。(皆満岁周去之。)以各段下平度,累加各段下平度,(満岁周去。)退则减之,(不及减,加岁周减之。)次复累加之,为各段中星。 推五星盈缩历 置中积,加历应及生合,満历率去之,余以度率而一为度。在历中已下为盈,已上减去历中为缩。置各星合伏下盈缩历,以段下限度累加之之満历中去之,盈  缩,缩 缩,缩 盈,即各段盈缩历。 盈,即各段盈缩历。推五星盈缩差 置各段盈缩历,以历策除之为策数,不尽,为策余。以其下损益分见立成。乘之,以历策而一,所得益加损减其盈缩积分,即盈缩差。金星倍之,⽔星三之。 推定积⽇ 置各段中积,以其段盈缩差盈加缩减之,即得。(満岁周去之,如中积不及减者,加岁周减之。)本段原无差者,借前段差加之,则金⽔二星,亦只用所得盈缩差,不用三之倍之。 推加时定⽇ 置定积⽇,以岁前天正冬至分加之,満纪法去之,余命甲子算外,即为定⽇。(视定积⽇会満岁周去者,用本年冬至,会加岁周减者,用岁前冬至。) 推所⼊月⽇ 置合伏下定积,以加天正闰馀満朔策除之,为月数。起岁前十一月,其不満朔策者,即⼊月已来⽇分也。视其月定朔甲子,与加时定⽇甲子相去即合伏⽇,累加相距⽇,満各月大小去之,即各段所⼊月⽇。 推定星 置各段中星,依推定积⽇法,以盈缩差加减之。 推加时定星 置定星,以岁前冬至加时⻩道⽇度加之,満周岁天去之。若定积⽇会加岁周者,用岁前⻩道⽇度。遇减岁周者,用本年⻩道目度,如原无中星度,段下亦无定星星及加时定星度分。 推加减定分 置定⽇小余,以其段初行率乘之,満万为分,所得诸段为减分,退段为加分。 推夜半定星及宿次 置加时定星,以加减定分加减之,为夜半定星。以⻩道积度钤减之,为夜半宿次。其留段即用时定星,为夜半一星。 推⽇度率 置各段定⽇,与次段定⽇相减为⽇率。次段不及减,加纪法减之。置各段夜半-定星,与次段夜半定星相减为度涨。次段不及减,加周天减之。凡近留之段,皆用留段加时定星,与本段夜半定星相减。如星度逆者,以后段减前段,即各得度率。 推平行分 置度率,以⽇率除之,即得。 推凡差及增减总差⽇差 以本段前后之平行分相减,为本段凡差。(凡五星之伏段及近留之迟段及退段,皆无凡差。)倍凡差,退一位为增减差。倍增减差为总差。置总差,以⽇率减一⽇除之为⽇差。(初⽇行分多,为减差。末⽇行分多,为加差。) 推初⽇行分末⽇行分 以增减差加减其段平行分,为初末⽇行分。视本段平行分与次段平行分相较,前多后少者,加为初,减为末。前少后多者,减为初,加为末。 推抚心差诸段为增减差总差⽇差 合伏者,置次段初⽇行分,加其⽇差之半,(亦次段⽇差。)为末⽇行分。晨伏、夕伏者,置前段(本段之前)。末⽇行分,加其⽇差之半,(亦前段⽇差。)为二伏初⽇行分。置伏段呼得初末⽇行分,皆与本段平行分相减,馀为增减差。又以增差加 减平行分,为初末⽇行分。视合伏末⽇行全较平行分,少则加,多则减,为初⽇行分。晨伏、夕伏初⽇行分较平行分,亦少加多减,为末⽇行分。木、火之晨迟末,土之晨迟,金之夕迟末,⽔之夕迟,皆置其前末⽇行分,锐其⽇差减之,(即前段⽇差。)馀为初⽇行分。木、火之夕迟初,土之夕迟,金之晨初,⽔之晨迟,皆置其后段初⽇行分,倍其⽇差减之,(后段⽇差。)馀为末⽇行分。木、火、土之夕伏,金、⽔之晨伏,皆置其前段末⽇行分,內加其前段⽇差之半,为钛段初⽇行分,皆与平行分相减,馀为增减差。木、火之晨退、夕退,置其平行分,退一位、六因之,为增减差。晨退减为初,加为末。夕退加为初,减为末。晨加夕减,二段相比较。金之夕退伏合伏,置其平行分,退一位,三因之折半。⽔之夕退伏合退伏,以平行分折半,各为增减差。金之夕退,置其平分,退一位,三在之折半。⽔之夕退伏合退伏,以平行分折半,各为增减差。金之夕退,置其后段禄⽇行分,减⽇差,(后段⽇差。)为末⽇行分。金之晨退,置其前段末⽇行分,减⽇差,(前段⽇差。)为初⽇行分。皆与平行分相减,馀为增减差。凡增减差,倍之为总差,以相距⽇率减一除之,为⽇差。其初末⽇行分有其一者,以增减差加减,更求其一,如伏段法,馀依前后平行分相较增减之。金、火之夕迟末,晨迟初,置其段平行分,以相距⽇率下不伦分乘之,(不伦分之秒,与平行之分对。)即为增减差。置平行分,夕者以增减差,加为初⽇行分,减为末⽇行分。晨者反是。 不伦分 (金、火星之夕迟末,与晨迟初,其增减差,多于平行分者,为不伦分也。) 十七⽇ 八十八秒八八五 十六⽇ 八十八秒二三一 十五⽇ 八十七秒四九六 十四⽇ 八十六秒七六一 推五星每⽇细行,置各段夜半宿次,以初⽇行分顺加退减之,为次⽇宿次。又以⽇差加减其初⽇行分,为每⽇行分,亦顺加退减于次⽇宿次,満⻩道宿次去之,至次段宿次而止,为每⽇夜半宿次。 推五星顺逆  宮时刻 视逐⽇五星细行,与⻩道十二宮界宿次同名,其度分又相近者以相减。视其馀分,在本⽇行分以下者,为 宮时刻 视逐⽇五星细行,与⻩道十二宮界宿次同名,其度分又相近者以相减。视其馀分,在本⽇行分以下者,为 宮在本⽇也。顺行者,以本⽇夜半星行宿次度分减宮界度分。退行者,以宮界度分减本⽇夜半星行宿次度分。扣以⽇周乘之为实,以本⽇行分为法,法除实,得数,依发敛加时法,得 宮在本⽇也。顺行者,以本⽇夜半星行宿次度分减宮界度分。退行者,以宮界度分减本⽇夜半星行宿次度分。扣以⽇周乘之为实,以本⽇行分为法,法除实,得数,依发敛加时法,得 宮时刻。 宮时刻。推五星伏见凡取伏见,伏者要在已下,见者要在已上。晨见晨伏者,置其⽇太 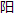 行度,內减各星行度。夕见夕伏者,置其⽇各星行度,內减太 行度,內减各星行度。夕见夕伏者,置其⽇各星行度,內减太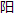 行度。即为其⽇晨昏伏见度。置本⽇伏见度,与次⽇伏见度相减,馀四而一,即得晨昏伏见分。视本⽇伏见度较次⽇伏见度为多者减,少者加。晨者,置本⽇伏见度,以伏见分加减之,为晨伏见度。夕者,三因伏见分,置伏见度加减之,为夕伏见度。视在各星伏见度上下取之。 行度。即为其⽇晨昏伏见度。置本⽇伏见度,与次⽇伏见度相减,馀四而一,即得晨昏伏见分。视本⽇伏见度较次⽇伏见度为多者减,少者加。晨者,置本⽇伏见度,以伏见分加减之,为晨伏见度。夕者,三因伏见分,置伏见度加减之,为夕伏见度。视在各星伏见度上下取之。步四馀 紫气周⽇一万零二百二十七⽇一七九二。 紫气度率二十八⽇,⽇行三分五七一四二九。 紫气至后策八千一百九十四万九六二三。 月孛周⽇三千二百三十一⽇九六八四。 月孛度率八⽇八四八四九二,⽇行十一分三零一三六一。 月孛至后策一千二百二十万四六五九。 罗计周⽇六千七百九十三⽇四四三二。 罗计度率一十八⽇五九九一零七七六,⽇行五分三七六六零二。 罗睺至后策五千三百三十三万六二一七。 计都至后策一千九百三十六万九零零一。 推四馀至后策 置中积,加各馀至后策,満周⽇去之,即得。 推四馀周后策 以至后策,减立成內各宿初末度积⽇,即得。 推四馀⼊各宿次初末度积⽇ 置各馀周后策,加⼊其年冬至分,満纪法去之,即各馀末度积⽇。紫气、月孛为各宿初,罗喉、计都为各宿末。气孛顺行,罗计逆行。 推四馀初末度积⽇所⼊月⽇ 置各馀周后策,加⼊天正闰馀満期策减之,起十一月至不満朔策,即所⼊月也。其初末度积⽇即満纪法去者。命甲子算外,为⽇辰小馀,以发敛求之为时刻。视定朔某甲女,即知⼊月已来⽇也。 推四馀每⽇行度 置各馀初末度积⽇,气孛以度率⽇累加之,至末度加其宿零⽇及分,即次宿之初度。罗计先加其宿零⽇及分,后以度率⽇累加之,即次宿之末度。徊以其大馀,命甲子算外为⽇辰。其  次宿,以小馀以敛为时刻。 次宿,以小馀以敛为时刻。推四馀  宮 以至后策减各宿 宮 以至后策减各宿 宮积⽇,馀为⼊某宮积中天正闰馀,満朔策去之,起十一月至不満朔策,即所⼊月。又置⼊宮积⽇,加冬至分,満纪法去之,为⽇辰,小馀以敛为时刻。视定朔甲子,即知 宮积⽇,馀为⼊某宮积中天正闰馀,満朔策去之,起十一月至不満朔策,即所⼊月。又置⼊宮积⽇,加冬至分,満纪法去之,为⽇辰,小馀以敛为时刻。视定朔甲子,即知 宮及时刻。 宮及时刻。▲紫气宿次⽇分立成(⼊箕初度。) (以下表格略) 至后策少者用前氐下积⽇,多者用后氐下积⽇。 wWW.igMXs.cOm |
|
| 上一章 明史 下一章 ( → ) |
| 元史金史辽史宋史新五代史旧五代史新唐书旧唐书北史南史 |
| 张廷玉等的免费历史小说《明史》由网友提供上传免费章节,闺蜜小说网只提供明史的存放,我们仅是一个广大网友免费阅读交流的小说平台,尽力最快速更新明史的免费章节,用心做最好的免费小说网。 |